Board coloration problem

Back to Tutorials | Use cases

Brief description

Given a rectangular board with dimension n*m, the goal is to color the cells such that any inner rectangle included inside the board doesn’t have all its corners colored with the same color. The goal is to minimize the number of colors used.

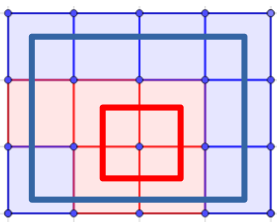
For example, this is not a valid solution of the 3*4 problem, because the red and blue rectangles have both their 4 corners having the same color:

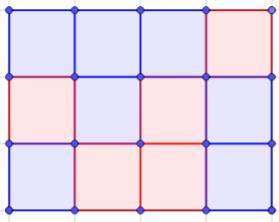
On the contrary, the following coloration is a valid solution of the 3*4 problem because every inner rectangle inside the board does not have a unique color for its corners:

CFN basic model

We create n*m variables, one for each square of the board, with domain size equal to n*m representing all the possible colors. We also create one variable for the number of colors.

We create hard quaternary constraints for every rectangle inside the board with a cost equal to 0 if the 4 variables have different values and a forbidden cost if not.

We then create hard binary constraints between the variable of the number of colors for each cell to fix the variable for the number of colors as an upper bound.

Then we create a soft constraint on the number of colors to minimize it.

Python model

The following code using pytoulbar2 library solves the board coloration problem with the first two arguments being the dimensions n and m of the board (e.g. “python3 boardcoloration.py 3 4”).

boardcoloration.py

import sys
from random import randint, seed
seed(123456789)
import pytoulbar2

try:
    n = int(sys.argv[1])
    m = int(sys.argv[2])
except:
    print('Two integers need to be in arguments: number of rows n, number of columns m')
    exit()

top = n*m + 1

Problem = pytoulbar2.CFN(top)

#create a variable for each cell
for i in range(n):
    for j in range(m):
        Problem.AddVariable('sq_' + str(i) + '_' + str(j), range(n*m))

#create a variable for the maximum of colors
Problem.AddVariable('max', range(n*m))

#quaterny hard constraints for rectangle with same color angles (encoding with forbidden tuples)
ConstraintTuples = []
ConstraintCosts = []
for k in range(n*m):
    #if they are all the same color 
    ConstraintTuples.append([k, k, k, k])
    ConstraintCosts.append(top)
#for each cell on the chessboard
for i1 in range(n):
    for i2 in range(m):
        #for every cell on the chessboard that could form a valid rectangle with the first cell as up left corner and this cell as down right corner
        for j1 in range(i1+1, n):
            for j2 in range(i2+1, m):
                # add a compact function with zero default cost and only forbidden tuples
                Problem.AddCompactFunction(['sq_' + str(i1) + '_' + str(i2), 'sq_' + str(i1) + '_' + str(j2), 'sq_' + str(j1) + '_' + str(i2), 'sq_' + str(j1) + '_' + str(j2)], 0, ConstraintTuples, ConstraintCosts)

#binary hard constraints to fix the variable max as an upper bound
Constraint = []
for k in range(n*m):
    for l in range(n*m):
        if k>l:
            #if the color of the square is more than the number of the max
            Constraint.append(top)
        else:
            Constraint.append(0)
for i in range(n):
    for j in range(m):
        Problem.AddFunction(['sq_' + str(i) + '_' + str(j), 'max'], Constraint)

#minimize the number of colors
Problem.AddFunction(['max'], range(n*m))

#symmetry breaking on colors
for i in range(n):
    for j in range(m):
        Constraint = []
        for k in range(n*m):
            if k > i*m+j:
                Constraint.append(top)
            else:
                Constraint.append(0)
        Problem.AddFunction(['sq_' + str(i) + '_' + str(j)], Constraint)

#Problem.Dump('boardcoloration.cfn')
Problem.CFN.timer(300)
res = Problem.Solve(showSolutions = 3)
if res:
    for i in range(n):
        row = []
        for j in range(m):
            row.append(res[0][m*i+j])
        print(row)
else:
    print('No solution found!')