Block modeling problem

Back to Tutorials | Use cases

Brief description

This is a clustering problem, occurring in social network analysis.

The problem is to divide a given directed graph G into k clusters such that the interactions between clusters can be summarized by a k*k 0/1 matrix M: if M[i,j]=1 then all the nodes in cluster i should be connected to all the nodes in cluster j in G, else if M[i,j]=0 then there should be no edge in G between the nodes from the two clusters.

For example, the following graph G is composed of 4 nodes:

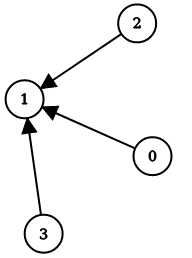
and corresponds to the following matrix:

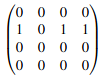
It can be perfectly clusterized into the following graph by clustering together the nodes 0, 2 and 3 in cluster 1 and the node 1 in cluster 0:

and this graph corresponds to the following M matrix:

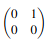
On the contrary, if we decide to cluster the next graph G’ in the same way as above, the edge (2, 3) will be ‘lost’ in the process and the cost of the solution will be 1.

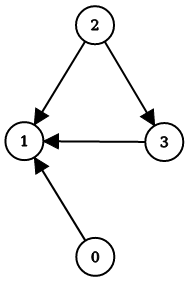
The goal is to find a k-clustering of a given graph and the associated matrix M that minimizes the number of erroneous edges.

A Mattenet, I Davidson, S Nijssen, P Schaus. Generic Constraint-Based Block Modeling Using Constraint Programming. CP 2019, pp656-673, Stamford, CT, USA.

CFN model

We create N variables, one for every node of the graph, with domain size k representing the clustering. We add k*k Boolean variables for representing M.

For all triplets of two nodes u, v, and one matrix cell M[i,j], we have a ternary cost function that returns a cost of 1 if node u is assigned to cluster i, v to j, and M[i,j]=1 but (u,v) is not in G, or M[i,j]=0 and (u,v) is in G. In order to break symmetries, we constrain the first k-1 node variables to be assigned to a cluster number less than or equal to their index

Data

You can try a small example simple.mat with optimum value equal to 0 for 3 clusters.

Perfect solution for the small example with k=3 (Mattenet et al, CP 2019)

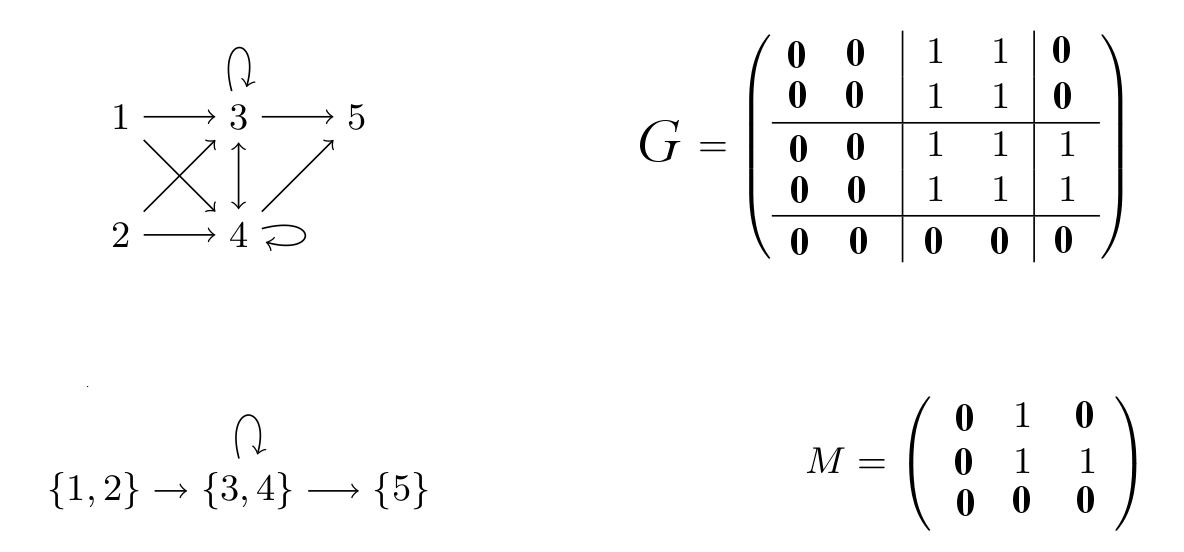
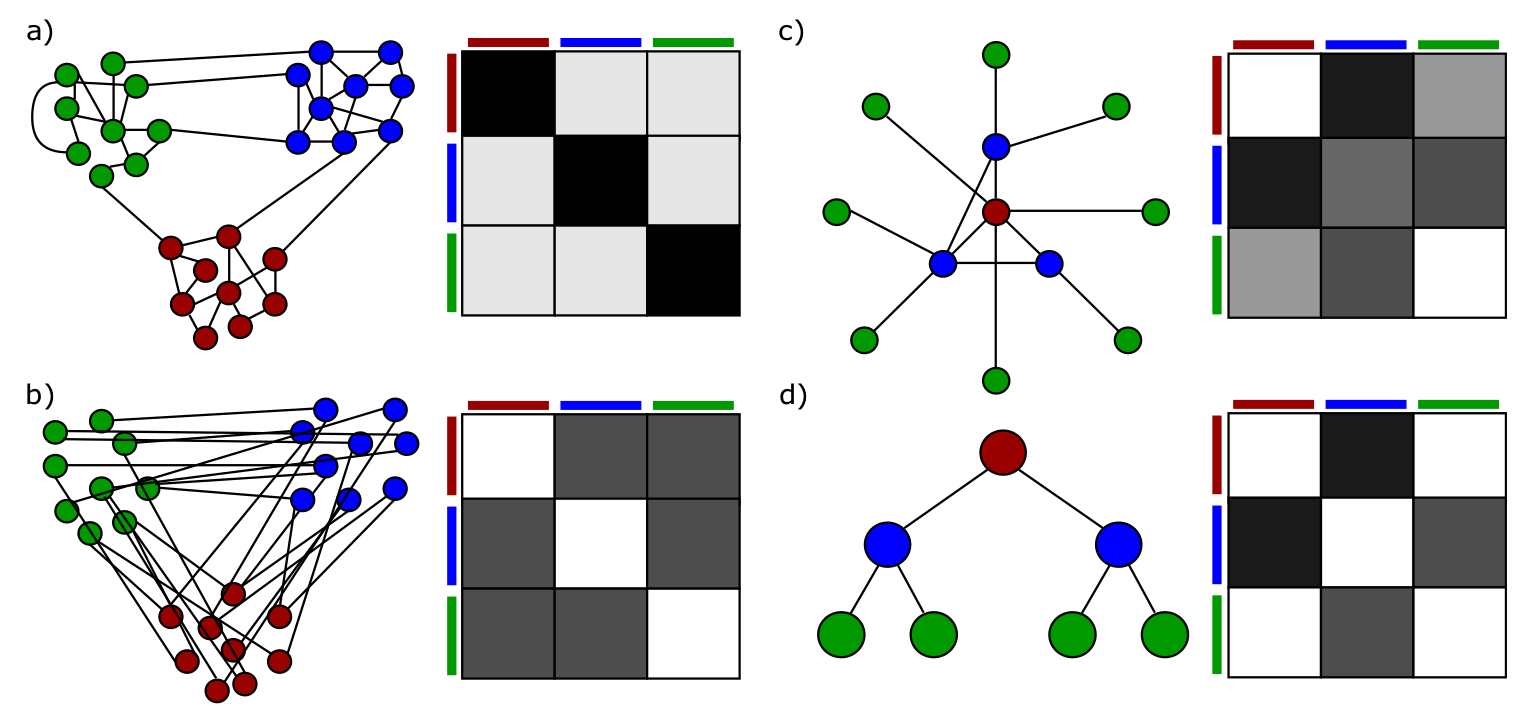
More examples with 3 clusters (Stochastic Block Models [Funke and Becker, Plos One 2019])

Python model

The following code using pytoulbar2 library solves the corresponding cost function network (e.g. “python3 blockmodel.py simple.mat 3”).

blockmodel.py

import sys
import pytoulbar2

#read adjency matrix of graph G
Lines = open(sys.argv[1], 'r').readlines()
GMatrix = [[int(e) for e in l.split(' ')] for l in Lines]

N = len(Lines)
Top = N*N + 1

K = int(sys.argv[2])

#give names to node variables
Var = [(chr(65 + i) if N < 28 else "x" + str(i)) for i in range(N)] # Political actor or any instance
#    Var = ["ron","tom","frank","boyd","tim","john","jeff","jay","sandy","jerry","darrin","ben","arnie"] # Transatlantic
#    Var = ["justin","harry","whit","brian","paul","ian","mike","jim","dan","ray","cliff","mason","roy"] # Sharpstone
#    Var = ["Sherrif","CivilDef","Coroner","Attorney","HighwayP","ParksRes","GameFish","KansasDOT","ArmyCorps","ArmyReserve","CrableAmb","FrankCoAmb","LeeRescue","Shawney","BurlPolice","LyndPolice","RedCross","TopekaFD","CarbFD","TopekaRBW"] # Kansas

Problem = pytoulbar2.CFN(Top)

#create a Boolean variable for each coefficient of the M GMatrix
for u in range(K):
    for v in range(K):
        Problem.AddVariable("M_" + str(u) + "_" + str(v), range(2))

#create a domain variable for each node in graph G
for i in range(N):
    Problem.AddVariable(Var[i], range(K))

#general case for each edge in G
for u in range(K):
    for v in range(K):
        for i in range(N):
            for j in range(N):
                if i != j:
                    ListCost = []
                    for m in range(2):
                        for k in range(K):
                            for l in range(K):
                                if (u == k and v == l and GMatrix[i][j] != m):
                                    ListCost.append(1)
                                else:
                                    ListCost.append(0)
                    Problem.AddFunction(["M_" + str(u) + "_" + str(v), Var[i], Var[j]],ListCost)



# self-loops must be treated separately as they involves only two variables
for u in range(K):
    for i in range(N):
        ListCost = []
        for m in range(2):
            for k in range(K):
                if (u == k and GMatrix[i][i] != m):
                    ListCost.append(1)
                else:
                    ListCost.append(0)
        Problem.AddFunction(["M_" + str(u) + "_" + str(u), Var[i]], ListCost)

# breaking partial symmetries by fixing first (K-1) domain variables to be assigned to a cluster number less than or equal to their index
for l in range(K-1):
    Constraint = []
    for k in range(K):
        if k > l:
            Constraint.append(Top)
        else:
            Constraint.append(0)
    Problem.AddFunction([Var[l]], Constraint)

Problem.Dump(sys.argv[1].replace('.mat','.cfn'))
Problem.CFN.timer(300)
res = Problem.Solve(showSolutions = 3)
if res:
    print("M matrix:")
    for u in range(K):
        Line = []
        for v in range(K):
            Line.append(res[0][u*K+v])
        print(Line)
    for k in range(K):
        for i in range(N):
            if res[0][K**2+i] == k:
                print("Node",Var[i],"with index",str(i),"is in cluster",str(res[0][K**2+i]))

toulbar2

An exact solver for cost function networks

Block modeling problem

Brief description

CFN model

Data

Python model