Golomb ruler problem

Back to Tutorials | Use cases

Brief description

A golomb ruler of order N is a set of integer marks 0=a1<a2<a3<a4<….<aN such that each difference between two ak’s is unique.

For example, this is a golomb ruler:

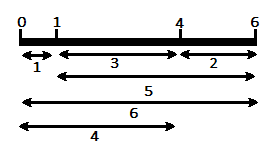
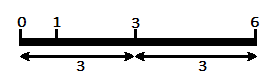
We can see that all differences are unique, rather than in this other ruler where 0-3 and 3-6 are both equal to 3.

The size of a golomb ruler is equal to aN, the greatest number of the ruler. The goal is to find the smallest golomb ruler given N.

CFN model

We create N variables, one for each integer mark ak. Because we can not create an AllDifferent constraint with differences of variables directly, we also create a variable for each difference and create hard ternary constraints in order to force them be equal to the difference. Because we do not use an absolute value when creating the hard constraints, it forces the assignment of ak’s variables to follow an increasing order.

Then we create an AllDifferent constraint on all the difference variables and one unary cost function on the last aN variable in order to minimize the size of the ruler. In order to break symmetries, we set the first mark to be zero.

Python model

The following code using pytoulbar2 library solves the golomb ruler problem with the first argument being the number of marks N (e.g. “python3 golomb.py 8”).

golomb.py

import sys
import pytoulbar2

N = int(sys.argv[1])

top = N**2 + 1

Problem = pytoulbar2.CFN(top)

#create a variable for each mark
for i in range(N):
    Problem.AddVariable('X' + str(i), range(N**2))

#ternary constraints to link new variables of difference with the original variables
for i in range(N):
    for j in range(i+1, N):
        Problem.AddVariable('X' + str(j) + '-X' + str(i), range(N**2))
        Constraint = []
        for k in range(N**2):
            for l in range(N**2):
                for m in range(N**2):
                    if l-k == m:
                        Constraint.append(0)
                    else:
                        Constraint.append(top)
        Problem.AddFunction(['X' + str(i), 'X' + str(j), 'X' + str(j) + '-X' + str(i)], Constraint)

Problem.AddAllDifferent(['X' + str(j) + '-X' + str(i) for i in range(N) for j in range(i+1,N)])

Problem.AddFunction(['X' + str(N-1)], range(N**2))

#fix the first mark to be zero
Problem.AddFunction(['X0'], [0] + [top] * (N**2 - 1))

#Problem.Dump('golomb.cfn')
Problem.CFN.timer(300)
res = Problem.Solve(showSolutions=3)
if res:
    ruler = '0'
    for i in range(1,N):
        ruler += ' '*(res[0][i]-res[0][i-1]-1) + str(res[0][i])
    print('Golomb ruler of size:',int(res[1]))
    print(ruler)