Weighted latin square problem

Back to Tutorials | Use cases

Brief description

The problem consists in assigning a value from 0 to N-1 to every cell of a NxN chessboard. Each row and each column must be a permutation of N values. For each cell, a random cost in (1…N) is associated to every domain value. The objective is to find a complete assignment where the sum of the costs associated to the selected values for the cells is minimized.

CFN model

We create NxN variables, one for every cell, with domain size N. An AllDifferent hard global constraint is used to model a permutation for every row and every column. Its encoding uses knapsack constraints. Unary cost functions containing random costs associated to domain values are generated for every cell. The worst possible solution is when every cell is associated with a cost of N, so the maximum cost of a solution is N**3, so forbidden assignments have cost k=N**3+1.

Example for N=4 in JSON .cfn format

{
  problem: { "name": "LatinSquare4", "mustbe": "<65" },
  variables: {"X0_0": 4, "X0_1": 4, "X0_2": 4, "X0_3": 4, "X1_0": 4, "X1_1": 4, "X1_2": 4, "X1_3": 4, "X2_0": 4, "X2_1": 4, "X2_2": 4, "X2_3": 4, "X3_0": 4, "X3_1": 4, "X3_2": 4, "X3_3": 4},
  functions: {
    {scope: ["X0_0", "X0_1", "X0_2", "X0_3"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X1_0", "X1_1", "X1_2", "X1_3"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X2_0", "X2_1", "X2_2", "X2_3"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X3_0", "X3_1", "X3_2", "X3_3"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},

    {scope: ["X0_0", "X1_0", "X2_0", "X3_0"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X0_1", "X1_1", "X2_1", "X3_1"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X0_2", "X1_2", "X2_2", "X3_2"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},
    {scope: ["X0_3", "X1_3", "X2_3", "X3_3"], "type:" salldiff, "params": {"metric": "var", "cost": 65}},

    {scope: ["X0_0"], "costs": [4, 4, 3, 4]},
    {scope: ["X0_1"], "costs": [4, 3, 4, 4]},
    {scope: ["X0_2"], "costs": [2, 1, 3, 2]},
    {scope: ["X0_3"], "costs": [1, 2, 3, 4]},
    {scope: ["X1_0"], "costs": [3, 1, 3, 3]},
    {scope: ["X1_1"], "costs": [4, 1, 1, 1]},
    {scope: ["X1_2"], "costs": [4, 1, 1, 3]},
    {scope: ["X1_3"], "costs": [4, 4, 1, 4]},
    {scope: ["X2_0"], "costs": [1, 3, 3, 2]},
    {scope: ["X2_1"], "costs": [2, 1, 3, 1]},
    {scope: ["X2_2"], "costs": [3, 4, 2, 2]},
    {scope: ["X2_3"], "costs": [2, 3, 1, 3]},
    {scope: ["X3_0"], "costs": [3, 4, 4, 2]},
    {scope: ["X3_1"], "costs": [3, 2, 4, 4]},
    {scope: ["X3_2"], "costs": [4, 1, 3, 4]},
    {scope: ["X3_3"], "costs": [4, 4, 4, 3]}}
}

Optimal solution with cost 35 for the latin 4-square example (in red, costs associated to the selected values) :

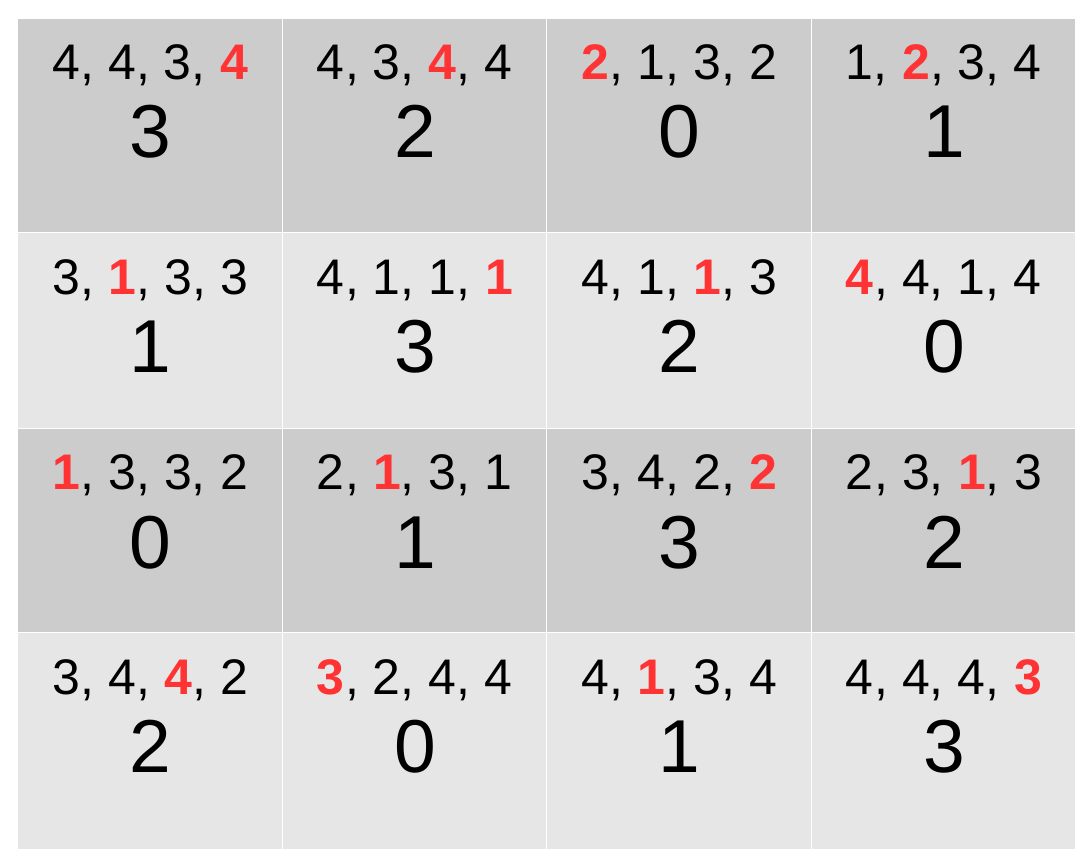
Python model

The following code using the pytoulbar2 library solves the weighted latin square problem with the first argument being the dimension N of the chessboard (e.g. “python3 latinsquare.py 6”).

latinsquare.py

import sys
from random import seed, randint
seed(123456789)
import pytoulbar2

N = int(sys.argv[1])

top = N**3 +1

Problem = pytoulbar2.CFN(top)

for i in range(N):
    for j in range(N):
        #Create a variable for each square
        Problem.AddVariable('Cell(' + str(i) + ',' + str(j) + ')', range(N))

for i in range(N):
    #Create a constraint all different with variables on the same row
    Problem.AddAllDifferent(['Cell(' + str(i) + ',' + str(j) + ')' for j in range(N)], encoding = 'salldiffkp')

    #Create a constraint all different with variables on the same column
    Problem.AddAllDifferent(['Cell(' + str(j) + ',' + str(i) + ')'for j in range(N)], encoding = 'salldiffkp')

#Random unary costs
for i in range(N):
    for j in range(N):
        ListConstraintsUnaryC = []
        for l in range(N):
            ListConstraintsUnaryC.append(randint(1,N))
        Problem.AddFunction(['Cell(' + str(i) + ',' + str(j) + ')'], ListConstraintsUnaryC)

#Problem.Dump('WeightLatinSquare.cfn')
Problem.CFN.timer(300)
res = Problem.Solve(showSolutions = 3)
if res and len(res[0]) == N*N:
    # pretty print solution
    for i in range(N):
        print([res[0][i * N + j] for j in range(N)])
    # and its cost
    print("Cost:", int(res[1]))