Weighted n-queen problem
Brief description
The problem consists in assigning N queens on a NxN chessboard with random costs in (1..N) associated to every cell such that each queen does not attack another queen and the sum of the costs of queen’s selected cells is minimized.
CFN model
A solution must have only one queen per column and per row. We create N variables for every column with domain size N to represent the selected row for each queen. A clique of binary constraints is used to express that two queens cannot be on the same row. Forbidden assignments have cost k=N**2+1. Two other cliques of binary constraints are used to express that two queens do not attack each other on a lower/upper diagonal. We add N unary cost functions to create the objective function with random costs on every cell.
Example for N=4 in JSON .cfn format
More details :

{
problem: { "name": "4-queen", "mustbe": "<17" },
variables: {"Q0":["Row0", "Row1", "Row2", "Row3"], "Q1":["Row0", "Row1", "Row2", "Row3"],
"Q2":["Row0", "Row1", "Row2", "Row3"], "Q3":["Row0", "Row1", "Row2", "Row3"]},
functions: {
{scope: ["Q0", "Q1"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q0", "Q2"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q0", "Q3"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q1", "Q2"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q1", "Q3"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q2", "Q3"], "costs": [17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17]},
{scope: ["Q0", "Q1"], "costs": [0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0]},
{scope: ["Q0", "Q2"], "costs": [0, 0, 0, 0, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0]},
{scope: ["Q0", "Q3"], "costs": [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 17, 0, 0, 0]},
{scope: ["Q1", "Q2"], "costs": [0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0]},
{scope: ["Q1", "Q3"], "costs": [0, 0, 0, 0, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0]},
{scope: ["Q2", "Q3"], "costs": [0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0]},
{scope: ["Q0", "Q1"], "costs": [0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0]},
{scope: ["Q0", "Q2"], "costs": [0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 0, 0, 0, 0]},
{scope: ["Q0", "Q3"], "costs": [0, 0, 0, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]},
{scope: ["Q1", "Q2"], "costs": [0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0]},
{scope: ["Q1", "Q3"], "costs": [0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 0, 0, 0, 0]},
{scope: ["Q2", "Q3"], "costs": [0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0, 17, 0, 0, 0, 0]},
{scope: ["Q0"], "costs": [4, 4, 3, 4]},
{scope: ["Q1"], "costs": [4, 3, 4, 4]},
{scope: ["Q2"], "costs": [2, 1, 3, 2]},
{scope: ["Q3"], "costs": [1, 2, 3, 4]}}
}
Optimal solution with cost 11 for the 4-queen example :
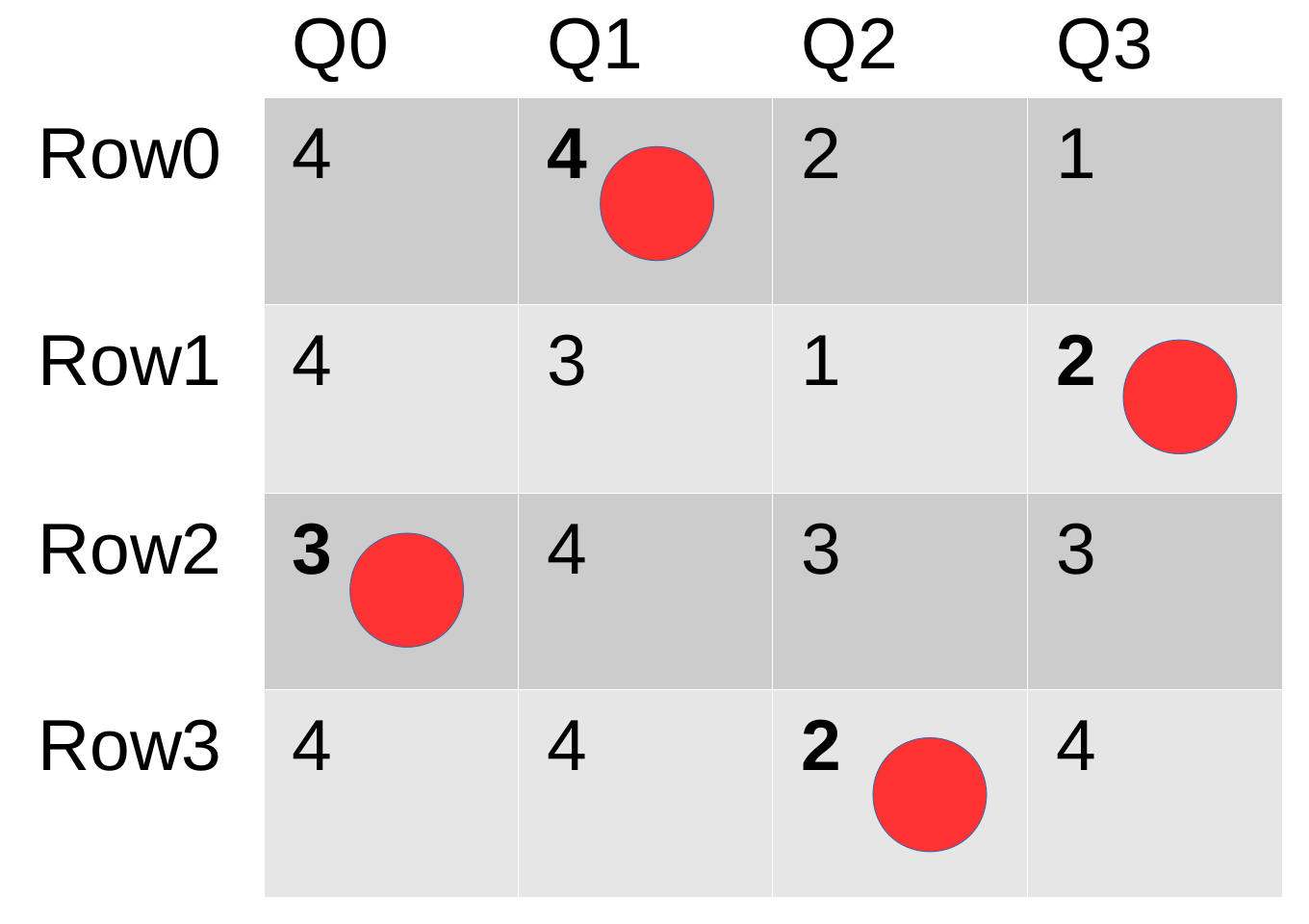
Python model
The following code using the pytoulbar2 library solves the weighted N-queen problem with the first argument being the number of queens N (e.g. “python3 weightedqueens.py 8”).
import sys
from random import seed, randint
seed(123456789)
import pytoulbar2
N = int(sys.argv[1])
top = N**2 +1
Problem = pytoulbar2.CFN(top)
for i in range(N):
Problem.AddVariable('Q' + str(i+1), ['row' + str(a+1) for a in range(N)])
for i in range(N):
for j in range(i+1,N):
#Two queens cannot be on the same row constraints
ListConstraintsRow = []
for a in range(N):
for b in range(N):
if a != b :
ListConstraintsRow.append(0)
else:
ListConstraintsRow.append(top)
Problem.AddFunction([i, j], ListConstraintsRow)
#Two queens cannot be on the same upper diagonal constraints
ListConstraintsUpperD = []
for a in range(N):
for b in range(N):
if a + i != b + j :
ListConstraintsUpperD.append(0)
else:
ListConstraintsUpperD.append(top)
Problem.AddFunction([i, j], ListConstraintsUpperD)
#Two queens cannot be on the same lower diagonal constraints
ListConstraintsLowerD = []
for a in range(N):
for b in range(N):
if a - i != b - j :
ListConstraintsLowerD.append(0)
else:
ListConstraintsLowerD.append(top)
Problem.AddFunction([i, j], ListConstraintsLowerD)
#Random unary costs
for i in range(N):
ListConstraintsUnaryC = []
for j in range(N):
ListConstraintsUnaryC.append(randint(1,N))
Problem.AddFunction([i], ListConstraintsUnaryC)
#Problem.Dump('WeightQueen.cfn')
Problem.CFN.timer(300)
res = Problem.Solve(showSolutions = 3)
if res:
for i in range(N):
row = ['X' if res[0][j]==i else ' ' for j in range(N)]
print(row)
# and its cost
print("Cost:", int(res[1]))