Frequency assignment problem with polarization
Brief description
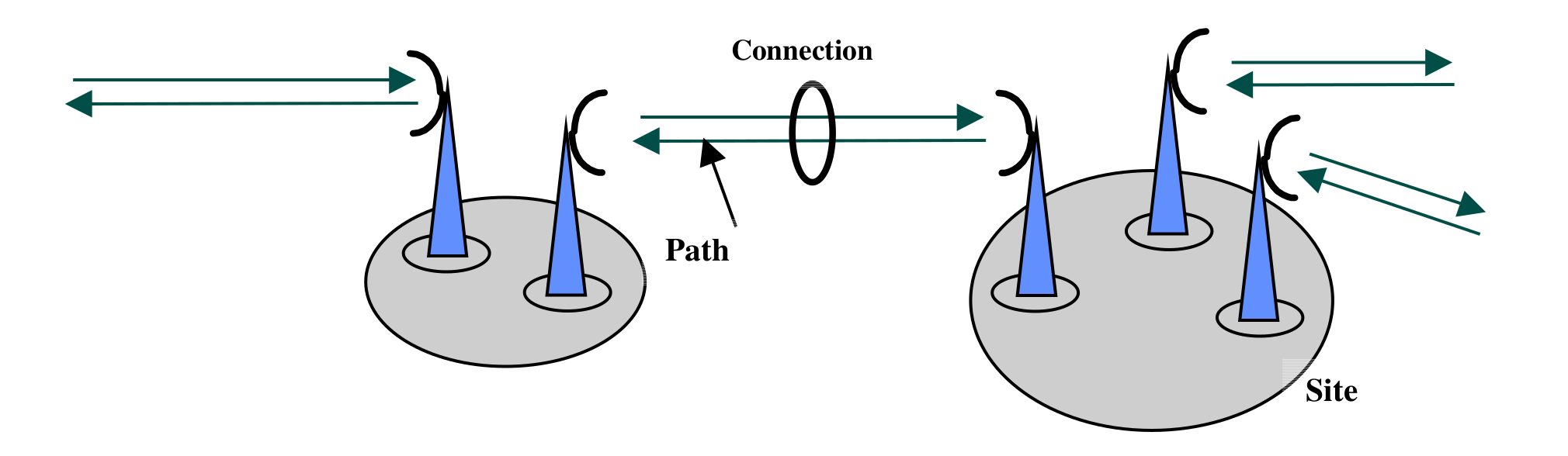
The previously-described Radio link frequency assignment problem has been extended to take into account polarization constraints and user-defined relaxation of electromagnetic compatibility constraints. The problem is to assign a pair (frequency,polarization) to every radio communication link (also called a path). Frequencies are integer values taken in finite domains. Polarizations are in {-1,1}. Constraints are :
(I) two paths must use equal or different frequencies (f_i=f_j or f_i<>f_j),
(II) the absolute difference between two frequencies should exactly be equal or different to a given number e (|f_i-f_j|=e or |f_i-f_j|<>e),
(III) two paths must use equal or different polarizations (p_i=p_j or p_i<>p_j),
(IV) the absolute difference between two frequencies should be greater at a relaxation level l (0 to 10) than a given number g_l (resp. d_l) if polarization are equal (resp. different) (|f_i-f_j|>=g_l if p_i=p_j else |f_i-f_j|>=d_l), with g_(l-1)>g_l, d_(l-1)>d_l, and usually g_l>d_l.
Constraints (I) to (III) are mandatory constraints, while constraints (IV) can be relaxed. The goal is to find a feasible assignment with the smallest relaxation level l and which minimizes the (weighted) number of violations of (IV) at lower levels. See ROADEF_Challenge_2001 .
The cost of a given solution will be calculated by the following formula: 10*k*nbsoft**2 + 10*nbsoft*V(k-1) + V(k-2) + V(k-3 ) + … + V0
where nbsoft is the number of soft constraints in the problem and k the feasible relaxation level and V(i) the number of violated contraints of level i.
CFN model
We create a single variable to represent a pair (frequency,polarization) for every radio link, but be aware, toulbar2 can only read str or int values, so in order to give a tuple to toulbar2 we need to first transform them into string. We use hard binary constraints to modelize (I) to (III) type constraints.
We assume the relaxation level k is given as input. In order to modelize (IV) type constraints we first take in argument the level of relaxation i, and we create 11 constraints, one for each relaxation level from 0 to 10. The first k-2 constraints are soft and with a violation cost of 1. The soft constraint at level k-1 has a violation cost 10*nbsoft (the number of soft constraints) in order to maximize first the number of satisfied constraints at level k-1 and then the other soft constraints. The constraints at levels k to 10 are hard constraints.
The initial upper bound of the problem will be 10*(k+1)*nbsoft**2 +1.
Data
Original data files can be download from ROADEF or fapp. Their format is described here. You can try a small example exemple1.in (resp. exemple2.in) with optimum 523 at relaxation level 3 with 1 violation at level 2 and 3 below (resp. 13871 at level 7 with 1 violation at level 6 and 11 below). See ROADEF Challenge 2001 results.
Python model
The following code solves the corresponding cost function network using the pytoulbar2 library and needs 4 arguments: the data file and the relaxation level (e.g. “python3 fapp.py exemple1.in 3”). You can also compile fappeval.c using “gcc -o fappeval fappeval.c” and download sol2fapp.awk in order to evaluate the solutions (e.g., “python3 fapp.py exemple1.in 3 | awk -f ./sol2fapp.awk - exemple1”).
import sys
import pytoulbar2
class Data:
def __init__(self, filename, k):
self.var = {}
self.dom = {}
self.ctr = list()
self.softeq = list()
self.softne = list()
self.nbsoft = 0
stream = open(filename)
for line in stream:
if len(line.split())==3 and line.split()[0]=="DM":
(DM, dom, freq) = line.split()[:3]
if self.dom.get(int(dom)) is None:
self.dom[int(dom)] = [int(freq)]
else:
self.dom[int(dom)].append(int(freq))
if len(line.split()) == 4 and line.split()[0]=="TR":
(TR, route, dom, polarisation) = line.split()[:4]
if int(polarisation) == 0:
self.var[int(route)] = [(f,-1) for f in self.dom[int(dom)]] + [(f,1) for f in self.dom[int(dom)]]
if int(polarisation) == -1:
self.var[int(route)] = [(f,-1) for f in self.dom[int(dom)]]
if int(polarisation) == 1:
self.var[int(route)] = [(f,1) for f in self.dom[int(dom)]]
if len(line.split())==6 and line.split()[0]=="CI":
(CI, route1, route2, vartype, operator, deviation) = line.split()[:6]
self.ctr.append((int(route1), int(route2), vartype, operator, int(deviation)))
if len(line.split())==14 and line.split()[0]=="CE":
(CE, route1, route2, s0, s1, s2, s3, s4, s5, s6, s7, s8, s9, s10) = line.split()[:14]
self.softeq.append((int(route1), int(route2), [int(s) for s in [s0, s1, s2, s3, s4, s5, s6, s7, s8, s9, s10]]))
self.nbsoft += 1
if len(line.split())==14 and line.split()[0]=="CD":
(CD, route1, route2, s0, s1, s2, s3, s4, s5, s6, s7, s8, s9, s10) = line.split()[:14]
self.softne.append((int(route1), int(route2), [int(s) for s in [s0, s1, s2, s3, s4, s5, s6, s7, s8, s9, s10]]))
self.top = 10*(k+1)*self.nbsoft**2 + 1
if len(sys.argv) < 2:
exit('Command line argument is composed of the problem data filename and the relaxation level')
k = int(sys.argv[2])
#collect data
data = Data(sys.argv[1], k)
Problem = pytoulbar2.CFN(data.top)
#create a variable for each link
for e in list(data.var.keys()):
domain = []
for i in data.var[e]:
domain.append(str(i))
Problem.AddVariable("X" + str(e), domain)
#hard binary constraints
for (route1, route2, vartype, operand, deviation) in data.ctr:
Constraint = []
for (f1,p1) in data.var[route1]:
for (f2,p2) in data.var[route2]:
if vartype == 'F':
if operand == 'E':
if abs(f2 - f1) == deviation:
Constraint.append(0)
else:
Constraint.append(data.top)
else:
if abs(f2 - f1) != deviation:
Constraint.append(0)
else:
Constraint.append(data.top)
else:
if operand == 'E':
if p2 == p1:
Constraint.append(0)
else:
Constraint.append(data.top)
else:
if p2 != p1:
Constraint.append(0)
else:
Constraint.append(data.top)
Problem.AddFunction(["X" + str(route1), "X" + str(route2)], Constraint)
#soft binary constraints for equal polarization
for (route1, route2, deviations) in data.softeq:
for i in range(11):
ListConstraints = []
for (f1,p1) in data.var[route1]:
for (f2,p2) in data.var[route2]:
if p1!=p2 or abs(f1 - f2) >= deviations[i]:
ListConstraints.append(0)
elif i >= k:
ListConstraints.append(data.top)
elif i == k-1:
ListConstraints.append(10*data.nbsoft)
else:
ListConstraints.append(1)
Problem.AddFunction(["X" + str(route1), "X" + str(route2)], ListConstraints)
#soft binary constraints for not equal polarization
for (route1, route2, deviations) in data.softne:
for i in range(11):
ListConstraints = []
for (f1,p1) in data.var[route1]:
for (f2,p2) in data.var[route2]:
if p1==p2 or abs(f1 - f2) >= deviations[i]:
ListConstraints.append(0)
elif i >= k:
ListConstraints.append(data.top)
elif i == k-1:
ListConstraints.append(10*data.nbsoft)
else:
ListConstraints.append(1)
Problem.AddFunction(["X" + str(route1), "X" + str(route2)], ListConstraints)
#zero-arity cost function representing a constant cost corresponding to the relaxation at level k
Problem.AddFunction([], 10*k*data.nbsoft**2)
#Problem.Dump('Fapp.cfn')
Problem.CFN.timer(900)
Problem.Solve(showSolutions=3)